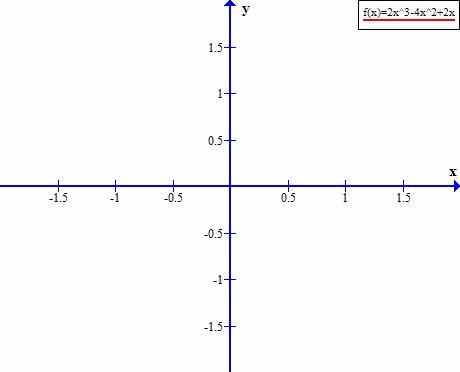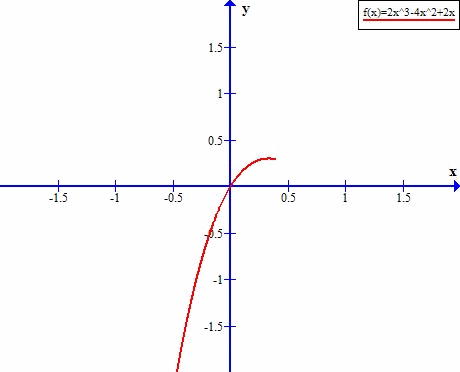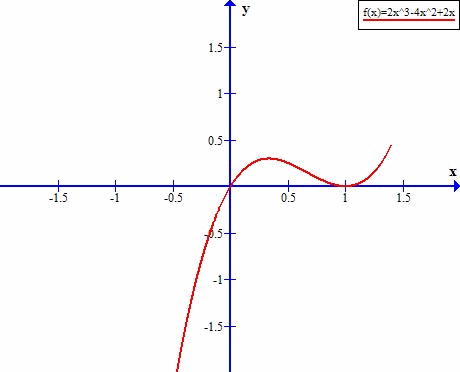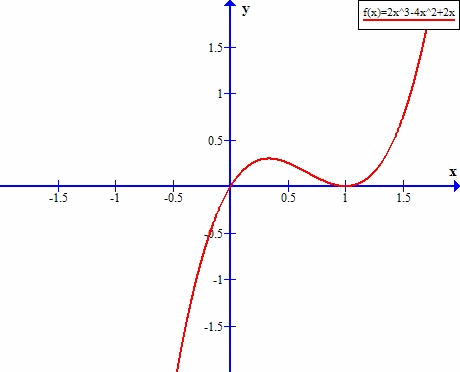
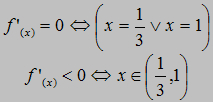Już wkrótce
Znając tylko wzór funkcji,
Będziesz potrafił
Naszkicować jej wykres.

Dowiesz się,
Jak z pomocą asymptot
Łatwiej narysować
Wykres funkcji.
Znając wzór funkcji
Wyznaczysz jej ekstrema,
Oraz ich wartości.
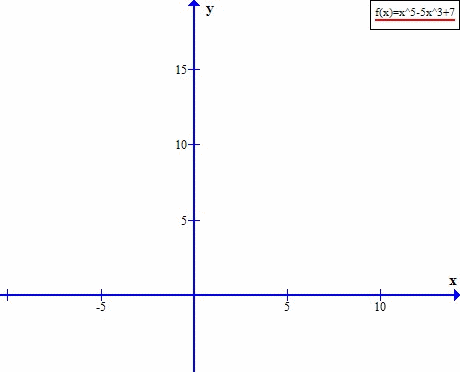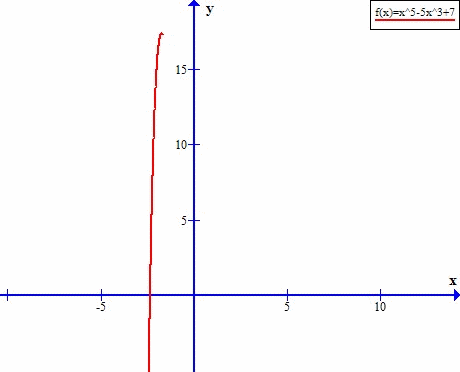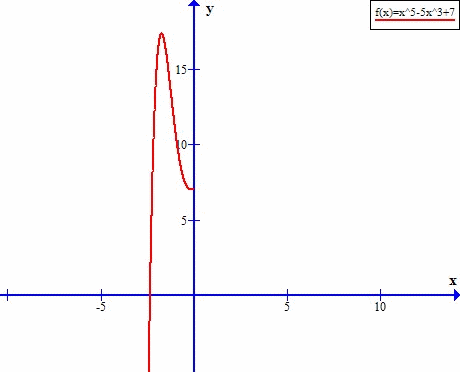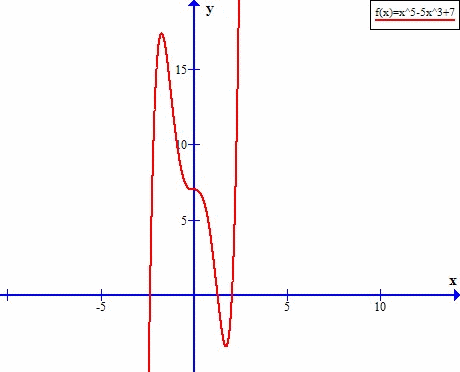
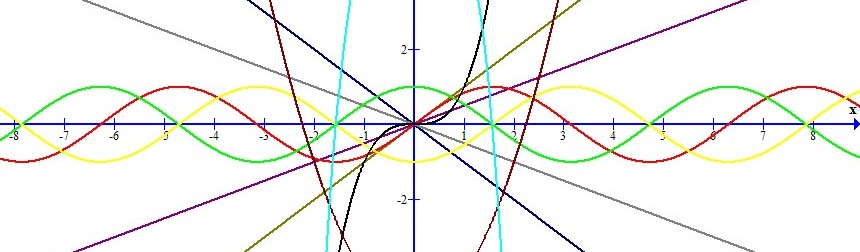
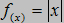 Przyjrzyjmy się tej funkcji w punkcie x=0
Przyjrzyjmy się tej funkcji w punkcie x=0
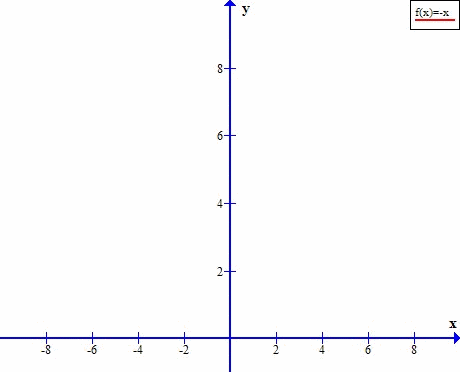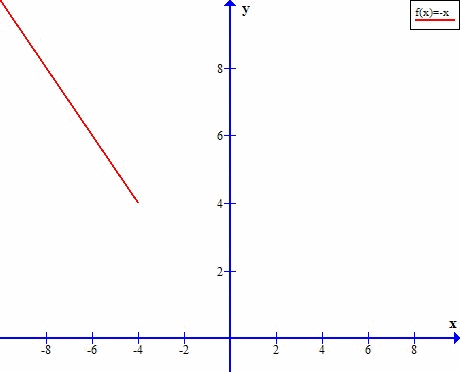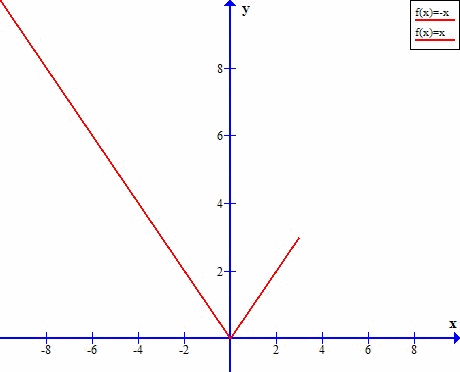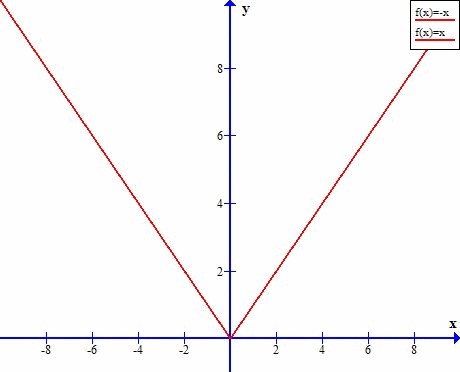 Funkcja z obydwu stron dąży do tej samej wartości.
Dlatego
Funkcja z obydwu stron dąży do tej samej wartości.
Dlatego 
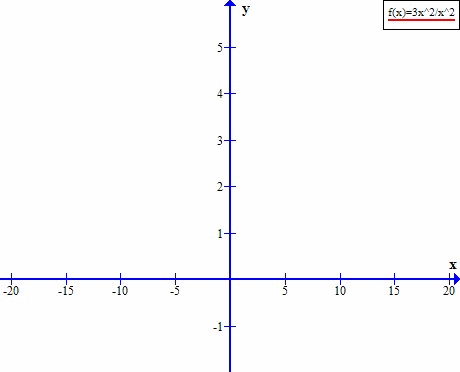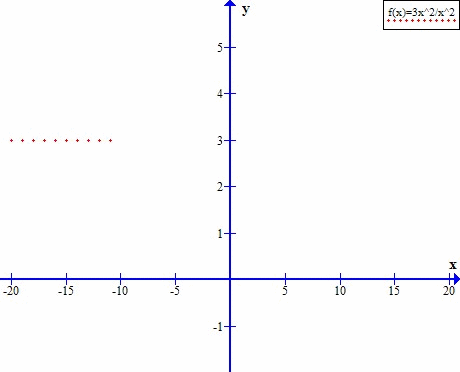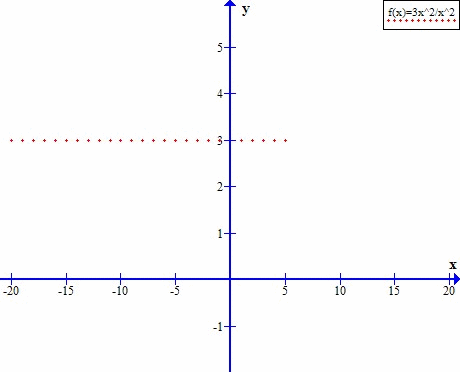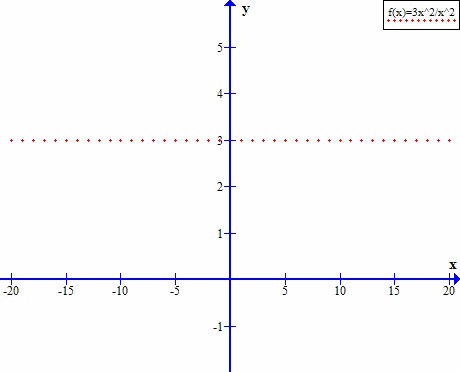 W ciągu stałym również występuje granica.
W ciągu stałym również występuje granica.
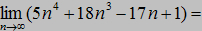
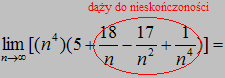
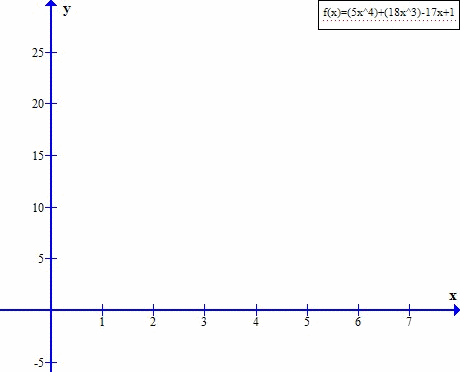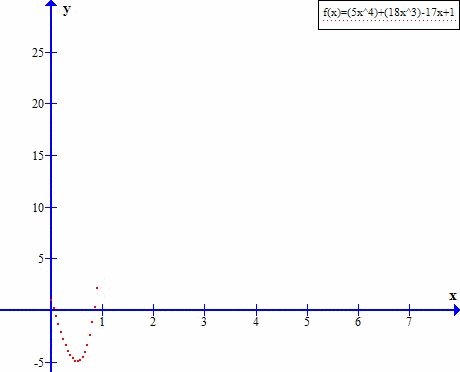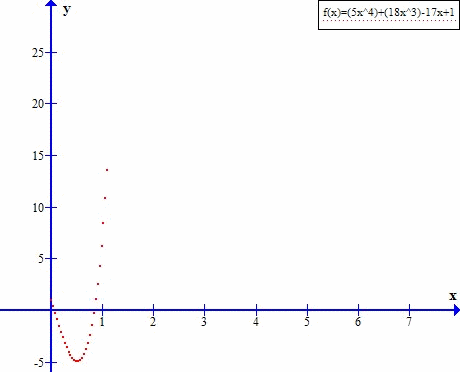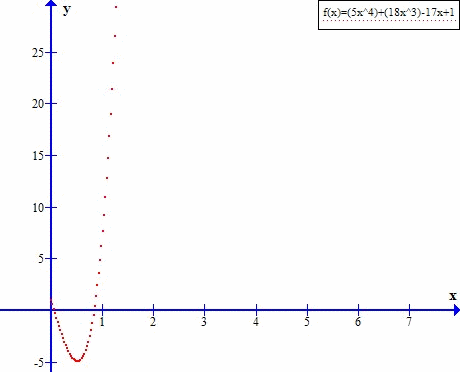 Wyraźnie widać, że ciąg zmierza do nieskończoności.
Wyraźnie widać, że ciąg zmierza do nieskończoności.
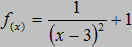 Asymptota w x=3
Asymptota w x=3
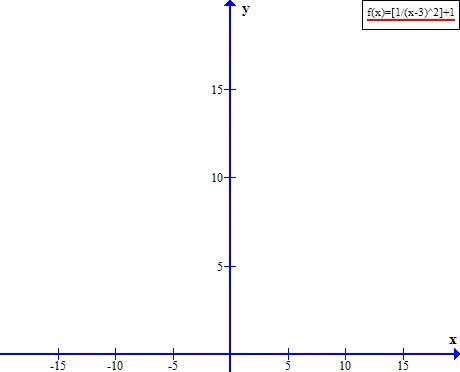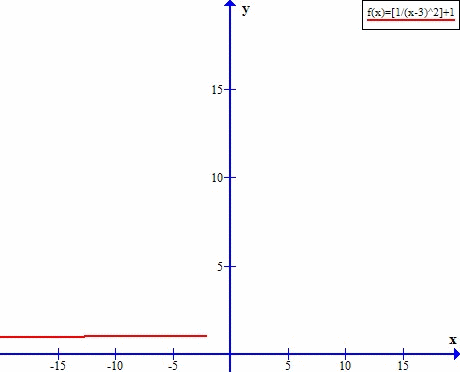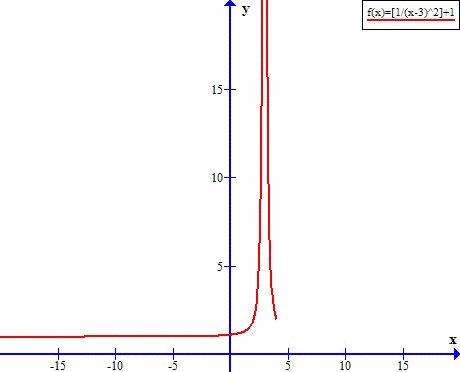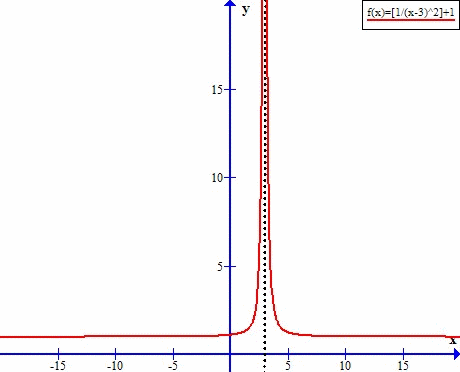
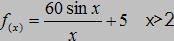 Asymptota w y=5
Asymptota w y=5

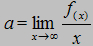 oraz
oraz
 Na przykład:
Na przykład:
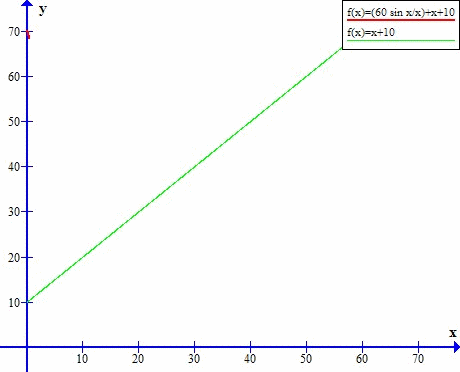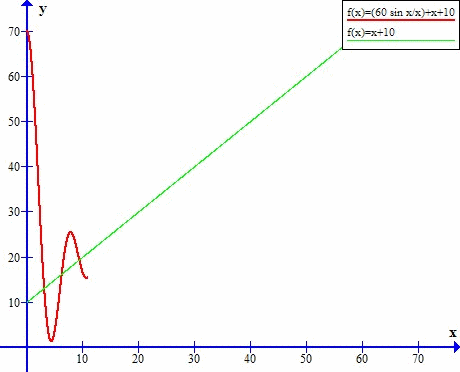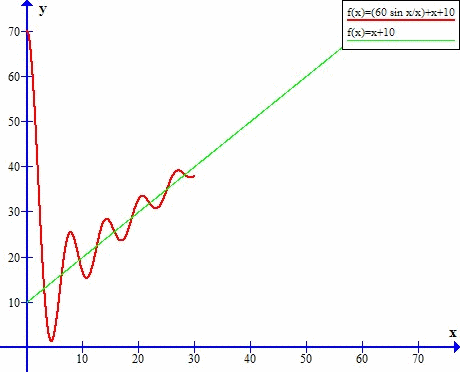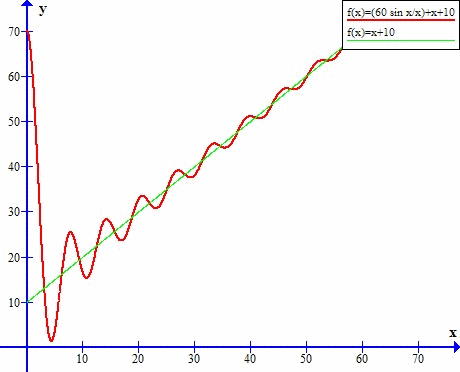
 Asymptota w y=x+10
Asymptota w y=x+10

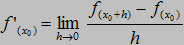 Obie definicje znaczą to samo. Różnią się tylko zapisem.
Obie definicje znaczą to samo. Różnią się tylko zapisem.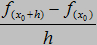 nazywany jest ułamkiem różnicowym,
dlatego wyprowadzanie funkcji pochodnej
określa się czasem jako "różniczkowanie".
nazywany jest ułamkiem różnicowym,
dlatego wyprowadzanie funkcji pochodnej
określa się czasem jako "różniczkowanie". Zobaczmy teraz te przekształcenia na kilku przykładach:
Zobaczmy teraz te przekształcenia na kilku przykładach:
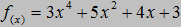
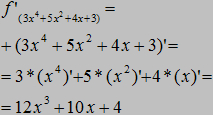
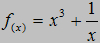
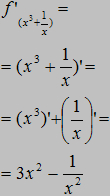
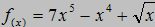
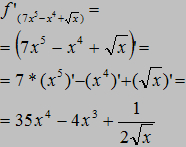
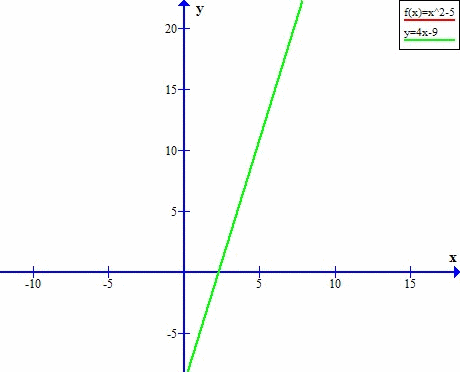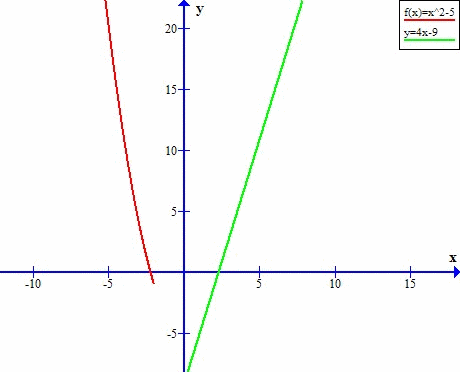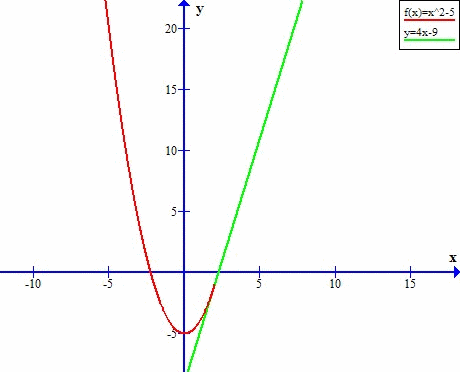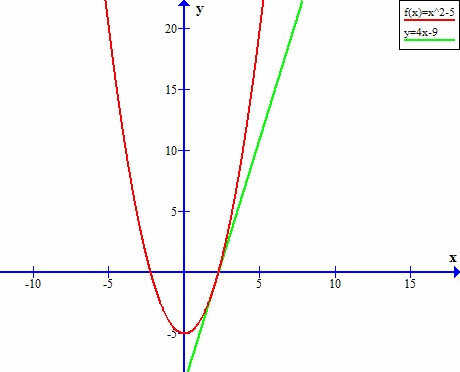
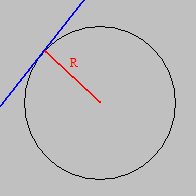 Zobaczmy, jak wyznaczyć styczną do wykresu funkcji!
Zobaczmy, jak wyznaczyć styczną do wykresu funkcji!
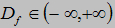 ,
, ,
,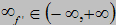 ,
,
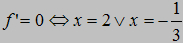
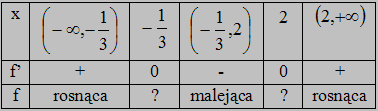
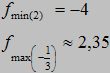
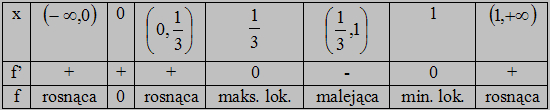
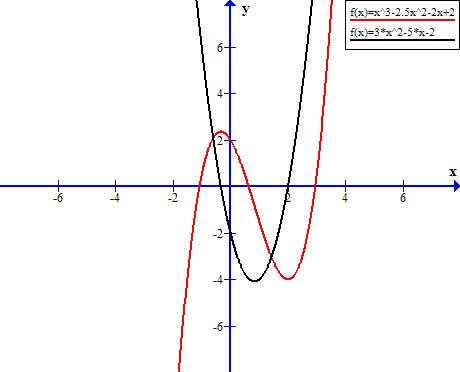 Kolorem czerwonym f(x)
Kolorem czarnym f'(x)
Kolorem czerwonym f(x)
Kolorem czarnym f'(x)
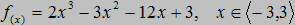
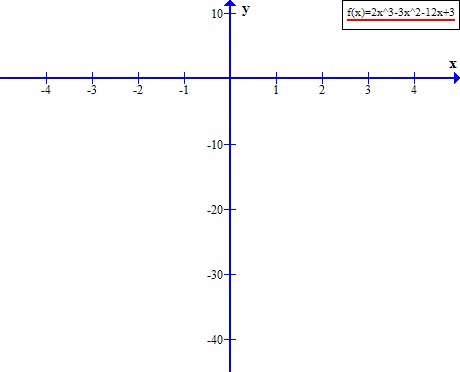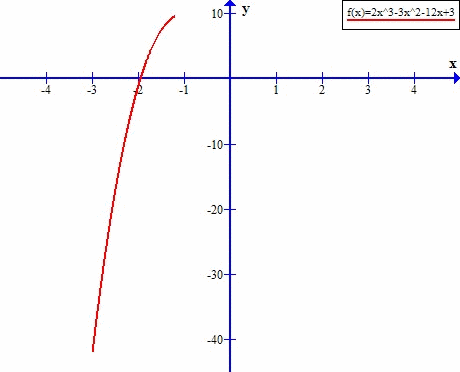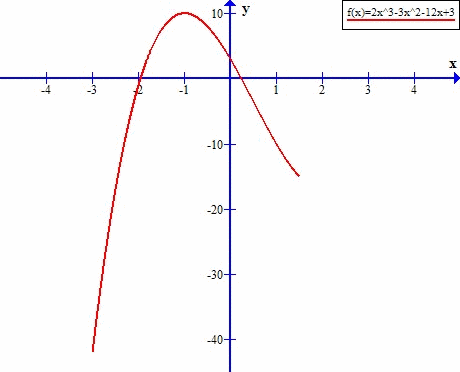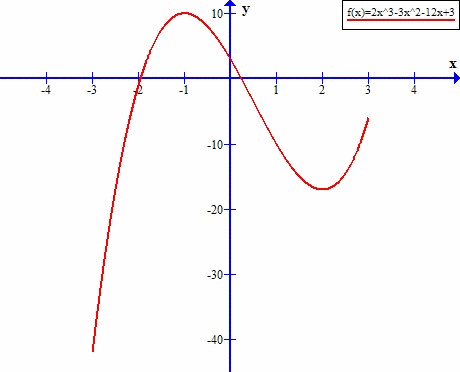
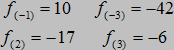
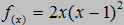
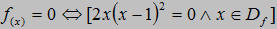 x=0 ۷ x=1
Punkty wspólne z osią X: (0,0), (1,0)
Z osią Y: (0,0)
x=0 ۷ x=1
Punkty wspólne z osią X: (0,0), (1,0)
Z osią Y: (0,0)
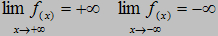 Wykres funkcji nie ma asymptoto pionowych, ani poziomych.
Wykres funkcji nie ma asymptoto pionowych, ani poziomych.
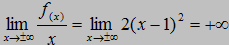 Brak także asymptot ukośnych.
Brak także asymptot ukośnych.
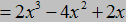 , stąd:
, stąd: